PCB기술 - PCB 배선 저항값의 빠른 추정

우리는 일반적으로 지루한 계산을 하기보다 인쇄 회로 기판의 전선이나 평면의 저항을 빠르게 추정해야 합니다. 배선 저항을 계산할 수 있는 사용 가능한 인쇄 회로 기판 레이아웃 및 신호 무결성 계산 프로그램이 있지만 때때로 설계 프로세스에서 빠르고 대략적인 추정 방법을 채택하기를 희망합니다.

"블록 통계"라고 하는 쉽게 할 수 있는 방법이 있습니다. 이 방법을 사용하면 모든 형상의 저항 값(약 10%)을 몇 초 안에 추정할 수 있습니다. 이 방법을 마스터하면 추정할 PCB 영역을 여러 블록으로 나눌 수 있습니다. 모든 블록의 수를 세어 전체 배선 또는 평면의 저항 값을 추정할 수 있습니다.

기본 개념

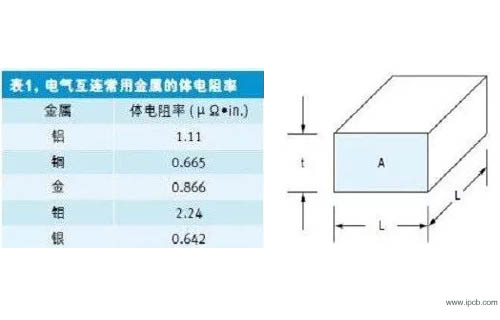
블록 통계의 핵심 개념은 모든 크기(두께로 결정됨)의 정사각형 인쇄 회로 기판의 저항 값이 다른 크기 블록의 저항 값과 동일하다는 것입니다. 양극 블록의 저항 값은 전도성 물질의 저항과 두께에만 의존합니다. 이 개념은 모든 유형의 전도성 재료에 적용할 수 있습니다. 표 1은 몇 가지 일반적인 반도체 재료와 이들의 벌크 저항을 보여줍니다.

인쇄회로기판에서 중요한 재료는 대부분의 회로기판의 원료인 구리입니다.

그림 1의 구리 블록부터 시작하겠습니다. 구리 블록의 길이는 l, 너비는 l(정사각형이므로), 두께는 t, 전류가 통과하는 구리박의 단면적 이다 구리 블록의 저항은 간단히 R = ρ L/A로 표현할 수 있습니다. 여기서 ρ는 25℃에서 구리의 고유 저항(재료 고유의 특성으로 0.67μΩ/in)입니다.


단, 단면 a는 길이 L과 두께 t의 곱입니다(a = LT). 분모의 L과 분자의 L은 서로 상쇄되어 r = ρ/T만 남게 됩니다. 따라서 구리 블록의 저항은 블록의 크기와 관련이 없으며 저항과 두께에만 의존합니다. 재료. 모든 크기의 구리 블록의 저항 값을 알고 있고 전체 경로를 분해하여 여러 블록으로 추정할 수 있다면 블록 수를 추가(계산)하여 와이어의 총 저항을 얻을 수 있습니다.

실현

이 기술을 구현하려면 인쇄 회로 기판 트레이스에 있는 블록의 저항 값과 동박 두께 사이의 함수 관계를 제공하는 표만 있으면 됩니다. 동박의 두께는 일반적으로 동박의 무게로 지정됩니다. 예를 들어 1온스. 구리는 1온스를 의미합니다. 평방 피트 당.

표 2는 4개의 일반적인 동박의 무게와 25℃와 100℃에서의 저항을 보여줍니다. 재료는 양의 온도 계수를 갖기 때문에 구리 저항은 온도가 증가함에 따라 증가합니다. 예를 들어, 이제 우리는 0.5oz의 저항을 알고 있습니다. 정사각형 동박은 블록 크기와 무관한 약 1m Ω입니다. 측정하고자 하는 인쇄회로기판 배선을 여러 개의 가상 블록으로 분해한 다음 이 블록을 더하면 배선 저항을 얻을 수 있습니다.

간단한 예를 들어보겠습니다. 그림 2는 너비가 1인치이고 길이가 12인치인 25℃에서 무게가 약 0.5oz인 직사각형 구리 와이어를 보여줍니다. 라우팅을 일련의 정사각형으로 분해할 수 있으며 각 정사각형은 길이가 1인치입니다. 따라서 총 12개의 사각형이 있습니다. 표 2에 따르면 각 0.5oz의 저항. 무거운 동박 블록은 1m Ω입니다. 이제 12개의 블록이 있으므로 배선의 총 저항은 12m Ω입니다.

돌리는 건 어때?

이해를 돕기 위해 이전 기사에서는 매우 간단한 예를 나열했는데 복잡한 점의 상황을 살펴보겠습니다.

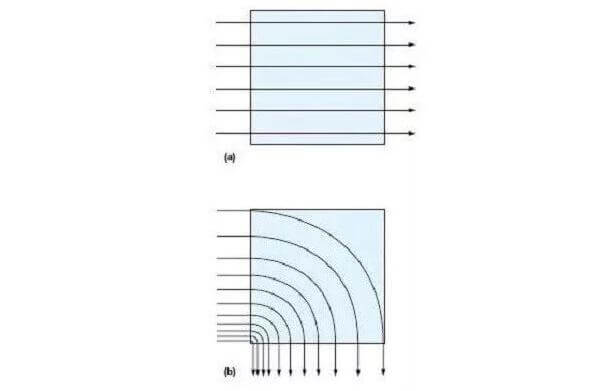
먼저 앞의 예에서 전류가 정사각형의 한 변을 따라 한쪽 끝에서 다른 쪽 끝으로 직선으로 흐른다고 가정했습니다(그림 참조). 그러나 전류가 직각으로 구부러지면(그림 3B의 정사각형과 같이) 상황이 다소 다릅니다.

앞의 예에서 우리는 전류가 정사각형의 한쪽 끝에서 다른 쪽 끝으로 직선으로 흐른다고 가정합니다(그림 참조). 전류가 직각 벤드를 취하는 경우(예: 그림 3B의 정사각형 직각), 블록의 왼쪽 아래 부분의 현재 경로가 오른쪽 위 부분의 경로보다 짧다는 것을 알 수 있습니다. 전류가 모서리를 통해 흐를 때 전류 밀도가 높기 때문에 모서리 정사각형의 저항은 0.56제곱으로만 계산할 수 있습니다.

이제 정사각형의 왼쪽 아래 부분의 현재 경로가 오른쪽 위 부분의 경로보다 짧음을 알 수 있습니다. 결과적으로 전류는 저항이 낮은 왼쪽 하단 영역에 밀집됩니다. 따라서 이 영역의 전류 밀도는 오른쪽 상단 영역의 전류 밀도보다 높을 것입니다. 화살표 사이의 거리는 전류 밀도의 차이를 나타냅니다. 결과적으로 모서리 사각형의 저항은 0.56제곱에 불과합니다.

마찬가지로 인쇄 회로 기판에 납땜된 커넥터를 약간 수정할 수 있습니다. 여기에서 커넥터 저항은 동박 저항에 비해 무시할 수 있다고 가정합니다.

커넥터가 평가할 동박 영역의 많은 부분을 차지하는 경우 해당 영역의 저항이 그에 따라 감소해야 함을 알 수 있습니다. 그림 5는 3단자 커넥터의 구조와 등가 블록의 계산을 보여줍니다(참조 1). 음영 처리된 영역은 동박 영역의 커넥터 핀을 나타냅니다.