PCB기술 - PCB 설계가 일반적으로 50옴 임피던스를 제어하는 이유

왜 PCB 설계가 일반적으로 50옴 임피던스를 제어합니까? ipcb가 답을 알려드리겠습니다.

PCB 설계 과정에서 배선 전에 우리는 일반적으로 설계하려는 항목을 쌓고 두께, 기판, 레이어 수 및 기타 정보에 따라 PCB 임피던스를 계산합니다. 계산 후 다음 그림을 얻을 수 있습니다.

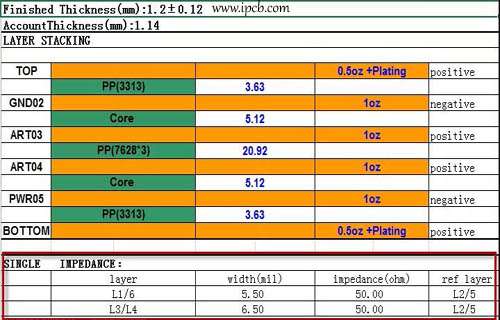
위의 그림에서 알 수 있듯이 위에서 설계된 단일 종단 네트워크는 일반적으로 50ohm으로 제어됩니다. 많은 사람들이 컨트롤이 25옴이나 80옴 대신 50옴을 기반으로 하는 이유를 묻습니다.

우선 기본 선택은 50옴이며 업계의 모든 사람들이 이 값을 수용합니다. 일반적으로 인정된 조직이 일정한 표준을 제정하고 그 표준에 따라 설계하는 것이 확실합니다.

전자 기술의 상당 부분은 군대에 있습니다. 우선 이 기술은 군에서 사용되며 점차 군에서 민간으로 이전된다.

마이크로웨이브 적용 초기인 2차 세계대전 당시 임피던스의 선택은 전적으로 사용의 필요에 달려 있었고 기준값이 없었습니다. 기술의 발전에 따라 경제성과 편의성의 균형을 위해 임피던스 규격을 부여할 필요가 있습니다.

미국에서는 일반적으로 사용되는 도관을 기존 스케일 로드와 수도관으로 연결합니다. 51.5옴은 매우 일반적이지만 사용되는 어댑터와 변환기는 50-51.5옴입니다. 이러한 문제를 해결하기 위해 mil에서 특별히 개발한 월이라는 조직(나중에 desc 조직)이 설립되었습니다. 종합적인 고민 끝에 50옴을 선정했고, 이에 관련된 도관을 제작하여 각종 케이블의 규격으로 바꾸었습니다.

이때 유럽 규격은 60옴이었다. 얼마 지나지 않아 업계에서 휴렛 패커드의와 같은 지배적인 회사의 영향으로 유럽인들은 변화할 수 밖에 없었습니다. 따라서 50옴은 결국 업계의 표준이 되었고, 하나의 관례가 되었습니다. 임피던스를 맞추기 위해 50옴 임피던스 규격에 따라 다양한 케이블로 연결된 PCB도 필요했다.

둘째, 일반 표준의 공식화는 PCB 생산 공정, 설계 성능 및 타당성을 종합적으로 고려하는 것을 기반으로 합니다.

PCB 생산 및 가공 기술의 관점에서 볼 때 대부분의 기존 PCB 제조업체의 장비를 고려하면 50ohm 임피던스의 PCB를 쉽게 생산할 수 있습니다.

임피던스 계산 과정에서 낮은 임피던스는 넓은 선폭과 얇은 매체 또는 큰 유전 상수를 필요로 하며 이는 현재의 고밀도 판을 위한 공간에서 충족하기 어려운 것입니다. 높은 임피던스는 더 얇은 선폭과 더 두꺼운 매체 또는 더 작은 유전 상수를 필요로 하므로 EMI 및 누화 억제에 도움이 되지 않습니다. 동시에 다층 판의 경우 대량 생산의 관점에서 처리 신뢰성도 매우 높습니다.

공통판(FR4 등) 및 공통 코어 기판을 사용하는 환경에서 50옴 임피던스를 제어하여 공통 판 두께(1mm, 1.2mm 등), 공통 선폭(4~ 10 ml)를 설계할 수 있어 판 공장에서 처리하기에 매우 편리하며 처리 장비에 대한 요구 사항이 그다지 높지 않습니다.

PCB 설계를 고려할 때 50ohm도 종합적으로 고려한 선택입니다. PCB 라우팅의 성능 면에서는 임피던스가 낮을수록 좋습니다. 주어진 선폭을 가진 전송 라인의 경우 평면에 가까울수록 해당 EMI가 감소하고 누화도 감소합니다.

그러나 전체 신호 경로의 관점에서 볼 때 핵심 요소인 칩의 구동 능력을 고려해야 합니다. 초기에는 대부분의 칩이 임피던스가 50옴 미만인 전송선로를 구동할 수 없었고 임피던스가 높은 전송선로는 구현이 쉽지 않아 50옴 임피던스를 채택했습니다.

따라서 일반적으로 단일 종단 신호 제어 PCB 임피던스의 기본값으로 50옴이 선택됩니다.